Ο “γύρος του θανάτου” σε Λωρίδα Mobius – Σάββας Γαβριηλίδης
ΜΟΝΟΝ Ο ΣΤΟ ΜΕΣΑΙΟ ΔΙΑΖΩΜΑ ΚΙΝΟΥΜΕΝΟΣ ΔΕΝ ΣΥΓΚΡΟΥΕΤΑΙ ΜΕ ΤΟ ΜΑΥΡΟ .!
Θέμα: Επεξήγηση του ζητούμενου .
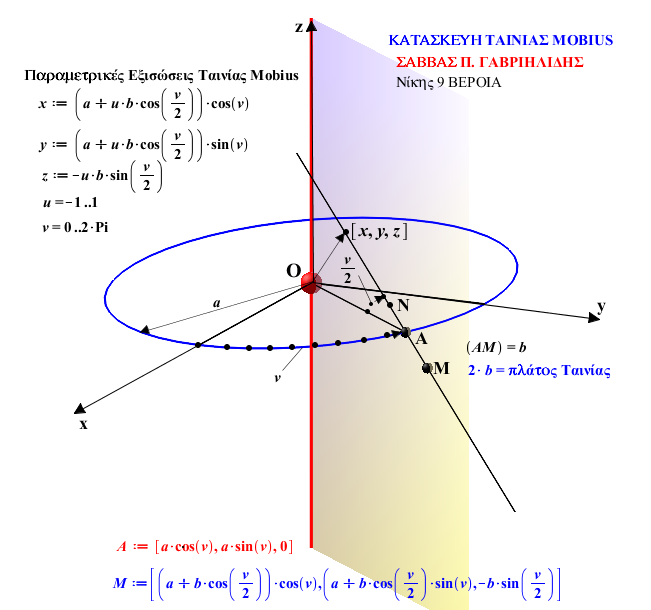
Έστω επί του συστήματος συντεταγμένων Oxyz κύκλος ακτίνας α , κείμενος στο επίπεδο xOy .
Το εικονιζόμενο επίπεδο περνάει από τον Άξονα Oz περιστρεφόμενο με δεδομένη γωνιακή ταχύτητα v . (Eίναι κάθετο στο επίπεδο του κύκλου ).
Ευθεία (AM) του ως άνω επιπέδου , τέμνει τον κύκλο στο σημείο A , περιστρεφόμενη περί αυτό το σημείο
με γωνιακή ταχύτητα ίση με το μισό της γωνιακής ταχύτητας περιστροφής του επιπέδου περί τον άξονα Oz .
Να βρούμε τις παραμετρικές εξισώσεις της Επιφάνειας που διαγράφει η Ευθεία κατά την κίνηση αυτή .
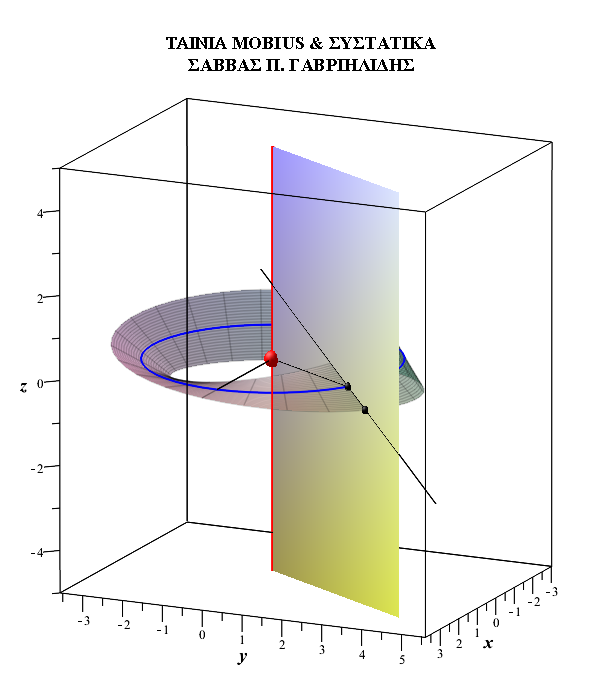
Αν Μ και Ν σημεία της ευθείας , τέτοια ώστε (ΑΜ)=(AN)=b , τότε το τμήμα (MN) διαγράφει κατά την κίνηση αυτή την γνωστή αναπτύξιμη Λωρίδα Mobius πλάτους 2b .
Η μαθηματική μελέτη
ΣΑΒΒΑΣ Π. ΓΑΒΡΙΗΛΙΔΗΣ
